|
计算机辅助公差标准化优化设计的研究
摘要:公差设计是产品设计的不可缺少的重要组成部分。标准化公差设计技术是保证产品实现标准化生产的关键技术之一。本文对产品标准化公差与制造成本的如何建模以及公差标准化算法的实现做出全面深入分析,提出了标准化的计算机辅助公差优化设计模型,以产品成本最低和装配成功率为目标函数,对产品公差设计进行标准化优化设计。计算机辅助公差标准化优化设计的研究,是目前国内外在制造系统领域的研究热点之一。
公差设计是产品设计的不可缺少的重要组成部分。产品设计过程分为三个阶段:系统设计、参数设计和公差设计。更为直观的,也可分成:功能设计、结构设计和公差设计。公差设计是保证产品设计功能实现的关键因素之一,而降低成本是获取经济效益的必要手段。因此,有必要对产品公差设计与制造周期成本的关系作出全面深入分析,并在此基础上研究如何保证产品功能和质量的前提下降低成本,即以产品成本最低为目标函数,对产品公差进行标准化优化设计。此方面的研究,也正是目前国内外在制造系统领域的研究热点之一。
对产品公差与成本进行建模是各种制造技术和理念的基础理论要求,是制造业发展的要求。本世纪制造业的大量新兴技术和理念,如并行工程,敏捷制造,质量工程等,无一不非常强调产品设计与成本之关系,均从不同角度,局部的或整体性地认识并以期改造制造系统。总之,从产品公差与成本关系进行建模能够为各种新技术提供强有力的基础理论支持,同时精确的量化模型,也能为计算机辅助技术提供基本理论依据。计算机辅助公差设计CAT(Computer-Aided Tolerance Design)也是实现CAD和CAM集成的核心技术之一,已成为影响设计和制造信息集成的瓶颈环节。自1988年以来,美国机械工程师学会ASME每年的设计自动化年会(Design Automation Conference)都设有专门的公差专题;国际生产工程协会CIRP也从1989年起,每隔一年召开一次全球性的计算机辅助公差设计专题讨论会;ASME和美国国家标准化研究所也联合召开了多次有关公差设计得学术会议;世界上其他工业化国家,如加拿大、法国、英国、德国、日本、瑞士和澳大利亚在公差设计方面也投入大量的人力物力。近10多年来,国际上有关公差分析的出版物也呈几何级数增加,出现不少新理论和新方法。一些国际著名杂志如IJPR、AMT和ASME的会刊每年都要刊登大量有关公差研究的学术论文。一些著名的CAD/CAM软件如IDEAS、PRO/E、UG也都增加了专门的公差分析模块。总之,在CAD/CAM技术已高度实用化的今天,人们已经意识到CAT技术已经成为制约CAD/CAM技术发展的瓶颈环节,需要集中力量进行深入研究。
一 标准化公差优化设计模型建模与算法实现
1.公差优化设计技术
公差是零件尺寸和几何参数的允许变动量。它是机械精度表达的具体表现,是机械装置的使用要求与制造经济性之间协调的产物、是机械产品设计和制造的重要技术指标。
公差设计(Tolerance Design)包括公差分析和公差分配,公差设计是建立在公差设计函数的基础之上的。所谓公差设计函数(Tolerance design function)就是指装配技术要求、产品功能要求等与有关尺寸之间的函数关系,如孔轴配合件的配合间隙的数学表达式。
所谓公差分析(Tolerance Analysis),也叫公差验证(Tolerance Verification),就是已知各组成环的尺寸和公差,确定最终装配后须保证的封闭环的公差。这时,组成环公差作为输入,封成环公差作为输出。当最终性能未满足时,重新修改输入公差。
所谓公差分配(Tolerance Distribution),也叫公差合成(Tolerance Systhesis),是指在保证产品装配技术要求下规定各组成环尺寸的经济合理的公差。公差的最优化分配(设计)法是指建立公差模型(加工成本公差模型、装配失效模型)和约束条件(装配功能要求、工序选择条件等),利用各种优化算法进行公差分配。公差优化设计实质上是一个以尺寸链(或传动链)组成的零部件制造成本最小为目标,以设计技术条件和预期装配成功率为约束的数学规划问题,也是一个多随机变量的优化问题。
众所周知,任何尺寸链均可转化为三环尺寸链,为此以三环尺寸链为例(如图1)来阐述公差优化设计。机械零件的尺寸受加工过程中许多因素的综合影响,因此可设定尺寸链的各尺寸互相独立且满足正态分布(否则,可通过数学转化而得到),则在一定的置信度为1-α 下,尺寸链的尺寸矢量
 可用其基本尺寸
可用其基本尺寸
 和标准矢量
和标准矢量
 来描述,即尺寸可表述为
来描述,即尺寸可表述为
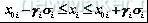 (其中:Yi 为第i个尺寸的置信系数,满足
(其中:Yi 为第i个尺寸的置信系数,满足
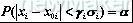 )且一般情况下,各尺寸的Yi 均相等,统一用Y 来表示),则尺寸公差为
)且一般情况下,各尺寸的Yi 均相等,统一用Y 来表示),则尺寸公差为
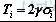 。一般而言,置信系统在公差设计时已预先确定,故公差正比于标准差,因此公差优化设计可转化为标准差设计问题。
。一般而言,置信系统在公差设计时已预先确定,故公差正比于标准差,因此公差优化设计可转化为标准差设计问题。
设计函数(Tolerance function
 )是尺寸链中各尺寸必须满足的装配或加工技术条件在数学上的表示。如图1,尺寸链的设计函数即装配技术条件函数可表述为:
)是尺寸链中各尺寸必须满足的装配或加工技术条件在数学上的表示。如图1,尺寸链的设计函数即装配技术条件函数可表述为:
 和
和
 。
。
公差域(tolerance region简称
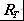 )是尺寸链中各尺寸公差带两端极限平面(三环尺寸链为直线)所围成的区域,在集合论中可表示为:
)是尺寸链中各尺寸公差带两端极限平面(三环尺寸链为直线)所围成的区域,在集合论中可表示为:
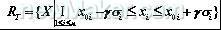 ,式中n(如图1中n=2) 为尺寸变量个数;X0i,
,式中n(如图1中n=2) 为尺寸变量个数;X0i,
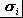 为尺寸变量Xi 的均值,标准差;Y 置信系数)。
为尺寸变量Xi 的均值,标准差;Y 置信系数)。

如图1中,该区域由方程为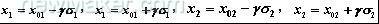 这4条直线所围成。 这4条直线所围成。
安全域(safe region简称Rs)是满足所有设计函数的空间点,即:
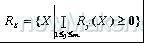 ,式中m为设计函数个数。如图1中,该区域为R1(x)=0和R2(x)=0 两直线所夹的区域。
,式中m为设计函数个数。如图1中,该区域为R1(x)=0和R2(x)=0 两直线所夹的区域。
如图1中,显而易见,可靠域、装配成功率要使尺寸矢量X落在图中有剖面线的区域内。对于任一尺寸链,该区域即为可靠域(reliable region 简称Rr )它是安全域Rs 、公差域Rt 的交集,在数学上可表示为:

 。该可靠域在三环尺寸链中为多边形或曲多边形(当设计函数Rj(X) 中有一个或一个以上为非线性函数时为曲多边形),四环以上尺寸链为多面体或曲多面体,称该域为广义可靠域(简称可靠域)。它是由广义设计函数(即装配技术条件函数与设计变量的公差范围方程式的统称,以下均简称为设计函数),即由安全域、公差域构成。尺寸矢量落在可靠域中的概率称为广义装配成功率(简称装配成功率)P(Rr)。不难发现,Rr依赖各尺寸的标准差;对于相同的变量、相同的置信度、相同的设计函数,惟独各个尺寸的标准差
。该可靠域在三环尺寸链中为多边形或曲多边形(当设计函数Rj(X) 中有一个或一个以上为非线性函数时为曲多边形),四环以上尺寸链为多面体或曲多面体,称该域为广义可靠域(简称可靠域)。它是由广义设计函数(即装配技术条件函数与设计变量的公差范围方程式的统称,以下均简称为设计函数),即由安全域、公差域构成。尺寸矢量落在可靠域中的概率称为广义装配成功率(简称装配成功率)P(Rr)。不难发现,Rr依赖各尺寸的标准差;对于相同的变量、相同的置信度、相同的设计函数,惟独各个尺寸的标准差
 不同,并不妨设
不同,并不妨设
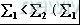 对应图1(a);对应图1(b)
对应图1(a);对应图1(b)
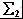 很显然,
很显然,
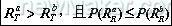 。若仅考虑装配技术条件函数即狭义设计函数,则称之为狭义设计函数,则狭义可靠域为:
。若仅考虑装配技术条件函数即狭义设计函数,则称之为狭义设计函数,则狭义可靠域为:
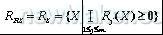 ,此时尺寸链的装配成功率称之为狭义装配成功率。
,此时尺寸链的装配成功率称之为狭义装配成功率。
加工成本——公差模型(Product tolerance-cost model),用C(T)或C(
 )来表示,就是用来描述加工成本与公差关系的数学表达式。对于一个装配尺寸链,若所有零件均按要求加工,其组成环公差值Ti(或标准差
)来表示,就是用来描述加工成本与公差关系的数学表达式。对于一个装配尺寸链,若所有零件均按要求加工,其组成环公差值Ti(或标准差
 ,一般来说置信系数Y 在设计前预先设定)减小时,尺寸链的装配成功率P(Rr)将增加,同时其加工总成本C(
,一般来说置信系数Y 在设计前预先设定)减小时,尺寸链的装配成功率P(Rr)将增加,同时其加工总成本C(
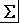 ) 也增加。因而如何合理分配公差,以便在满足约束条件下使得总成本最低,这是一个需要优化的问题。数学上(用标准差来表征公差)可表示为: MinC(
) 也增加。因而如何合理分配公差,以便在满足约束条件下使得总成本最低,这是一个需要优化的问题。数学上(用标准差来表征公差)可表示为: MinC(
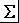 ),约束条件为:
),约束条件为:
 式中:Rr为可靠域;
式中:Rr为可靠域;
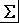 为尺寸矢量X所对应的标准差矢量;Pu为预期装配成功率;fx(X)为多随机变量的联合概率密度函数。
为尺寸矢量X所对应的标准差矢量;Pu为预期装配成功率;fx(X)为多随机变量的联合概率密度函数。
机械零件的尺寸受加工过程中许多因素的综合影响,因此可设定尺寸链的各尺寸互相独立且满足正态分布(否则,可通过数学转化而得到),因而上式可转化MinC(
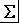 ),约束条件为:
),约束条件为:
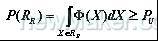 。式中:
。式中:

为服从正态分布的多随机变量的联合概率密度函数。
当优化变量较少时,Rr较简单,可直接通过数值积分来完成其装配成功率的估算;但当优化变量较多时或设计函数为非线性时,一般Rr是一个复杂的区域,难以采用数值积分法来估算。且
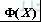 也不是一个简单的初等函数,因而要在Rr上对
也不是一个简单的初等函数,因而要在Rr上对
 进行体积分是一项相当困难的工作,为此有必要开展公差优化设计模型的研究,以寻求最佳的公差优化设计模型。
进行体积分是一项相当困难的工作,为此有必要开展公差优化设计模型的研究,以寻求最佳的公差优化设计模型。
2.标准化公差优化设计模型建模
公差优化设计可根据公差域的连续性,分为连续公差和离散公差模型优化设计两大类。在产品设计中,零件公差应尽量优先采用是国际推荐值,这就要进行标准化公差优化设计,一般有两种方法:(1)先采用连续公差优化设计方法,再将其进行圆整处理;(2)直接采用离散优化设计。很显然采用第一种方法,尽管其连续解满足设计函数,但其圆整结果可能会处于公差设计的可靠域外,从而不满足设计函数,或造成该离散解的加工成本并非所有可行解域内的最小值。因此有必要开展公差离散模型的标准化优化设计研究,以下结合实例具体介绍公差离散模型的标准化优化设计的算法。
现以一个孔、轴组成的间隙配合为例,若其配合尺寸为Ø85mm,且用于一般的传动中,假设孔、轴的公差等级选择范围为IT6~IT11,即其公差值可从22µm,35µm,54µm,87µm,140µm,220µm中选取,因此对该尺寸链的离散公差优化设计实质是按IT6~IT11六个公差等级在孔、轴36种可能组合中选取一组即满足装配技术条件、又使得其加工成本在所有满足装配技术条件的可能组合中最小的公差组合。其数学描述为
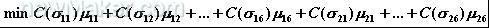
约束条件为:
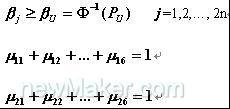
式中
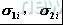 为孔、轴的第I种可能选取的标准差,I=1,2,3,4,5,6;
为孔、轴的第I种可能选取的标准差,I=1,2,3,4,5,6;
 为孔、轴的第I种标准差可能的选取系数,当某一标准差选中时,其值为1,否则为0。
为孔、轴的第I种标准差可能的选取系数,当某一标准差选中时,其值为1,否则为0。
对于一般尺寸链的离散公差优化设计可以将上式加以推广,则标准化公差优化设计模型表达为:
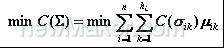
约束条件为:
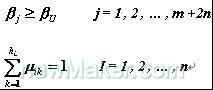
式中
 为尺寸Xi的第k个离散公差值所对应的标准差;Hi为尺寸Xi的可选择的标准差个数; m 为设计函数个数;n为尺寸变量个数;
为尺寸Xi的第k个离散公差值所对应的标准差;Hi为尺寸Xi的可选择的标准差个数; m 为设计函数个数;n为尺寸变量个数;
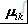 为尺寸Xi所选择的第k个标准差的选择系数,当
为尺寸Xi所选择的第k个标准差的选择系数,当
 被选时为1,否则为0。
被选时为1,否则为0。
第一个约束条件被称之为可靠性约束条件,第二个约束条件被称之为选择约束条件,很显然上式所描述的离散公差优化设计已转化为一个整数规划问题。
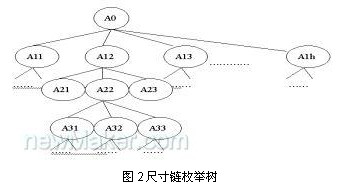
3.标准化公差优化设计的分枝估界法
分枝估界法已成功的解决了整数规划问题,其过程为:对有约束条件的最优化问题(其可行解为有限数)的所有可行域空间反复地分割越来越小的子集(即分枝),并且计算每一个子集的的下界(即估界)。在每次分枝之后,凡是界限越出已知可行解值的那些子集就不再进一步分枝。这样可行域可删除许多子集。这样可行域内可以删除许多子集。这种分枝继续进行知道找到可行解为止,这样可行解的值不大于任何子集的界限。由于公差与加工成本、公差与约束条件函数的可靠性指标之间的反向变化,因而采用了具有特色的分枝和剪枝技术的分枝估界算法。若尺寸链有n个尺寸,其枚举树如图2所示,该树共有n支。第I层单个节点的分枝数Hi 代表第I个尺寸公差等级可供选择的数,每个节点可用n维序列矢量Q来描述,如Q=[1,3,Hi,0,…,0]
 表示为该节点的各尺寸标准差的选取情况为:第一个尺寸选取第一种供选择的标准差、第二个尺寸选取第三种供选择的标准差、第三个尺寸选取第H3 种供选择的标准差、其余尺寸均尚未选取任何标准差;Q=[22,,2,2,…,2]
表示为该节点的各尺寸标准差的选取情况为:第一个尺寸选取第一种供选择的标准差、第二个尺寸选取第三种供选择的标准差、第三个尺寸选取第H3 种供选择的标准差、其余尺寸均尚未选取任何标准差;Q=[22,,2,2,…,2]
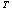 所有尺寸均选取第二种供选择的标准差。且在枚举树中似的同一父节点(某一节点与它连接的分枝之间存在父子关系)的各分枝中左节点的公差大于右节点的公差,从而使得左节点的加工成本和可靠性均小于右接点的值。利用深度优先原则来搜索该枚举树。可采用随机方法在可行域中产生一个满足约束条件的初始可行解,然后根据左右节点的加工成本、可靠性指标与公差之间的递减关系进行分枝和剪枝,其算法为:
所有尺寸均选取第二种供选择的标准差。且在枚举树中似的同一父节点(某一节点与它连接的分枝之间存在父子关系)的各分枝中左节点的公差大于右节点的公差,从而使得左节点的加工成本和可靠性均小于右接点的值。利用深度优先原则来搜索该枚举树。可采用随机方法在可行域中产生一个满足约束条件的初始可行解,然后根据左右节点的加工成本、可靠性指标与公差之间的递减关系进行分枝和剪枝,其算法为:
(1)产生一个待选序列,其生成顺序
 ,并产生初始可行解Q ,计算此时尺寸链的总加工成本C,并令优化成本和优化成本序列为Cu=C,Qu=Q。
,并产生初始可行解Q ,计算此时尺寸链的总加工成本C,并令优化成本和优化成本序列为Cu=C,Qu=Q。
(2)判断待选序列是否为空?若是,输出优化结果Cu,Qu。
(3)按先进后出的原则,从待选序列中选出一个节点
 计算该子问题的成本下界
计算该子问题的成本下界
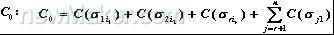 并判断
并判断
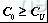 ?是,转入(2)。
?是,转入(2)。
本步骤即为分界,采用的策略即为估界原则。
(4)根据上一被选择节点
 ,产生一个新的节点
,产生一个新的节点
 ,并判断该节点是否满足装配技术条件?否,剪去该节点同一父节点的所有分枝。转向(2)。
,并判断该节点是否满足装配技术条件?否,剪去该节点同一父节点的所有分枝。转向(2)。
本步骤即为分枝,采用的策略即为分枝原则。
(5)判断r = n ? 是,计算优化加工成本
 ,并令Qu=Q,转向(2)。
,并令Qu=Q,转向(2)。
(6)令Cu=C0,Qu=Q,并将本节点的所有分枝子节点(该节点的下一层与其直接相连的所有节点),进入待选序列,其进入顺序为
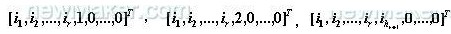 ,转入(2)。
,转入(2)。
三 基于UG平台的开发方案
1基于UG的计算机辅助公差设计模块的尺寸链信息获取模块
在UG环境下,通过对话框,由客户输入封闭环和各个组成环参数信息,再由计算机自动进行公差分配和公差分析工作,可以反复计算分析,直到满意为止,还可随时修改尺寸链,增加必要的组成环或者删减冗余的组成环,重新进行尺寸链的分析和计算。这样就实现了交互性公差设计,交互输入尺寸链信息,不需要先建立装配模型,保证尺寸链正确性,可随时修改尺寸链。
输入尺寸链参数后,应用公差分析模块进行公差分析,可以选择不同的方法进行公差分析,其中有标准化公差设计模块。图3为基于UG平台的计算机辅助公差分析模块界面。
应用公差分析模块进行公差分析:尺寸链的参数输入:打开UG,选取[公差设计]菜单的[公差分析]子菜单,弹出对话框,按下“确定封闭环参数”按纽,弹出输入封闭环参数对话框,这时要求输入封闭环参数(见图3中左面的对话框);完成了封闭环参数的输入后,按下“输入组成环参数”按纽,弹出输入组成环参数对话框,要求输入各个组成环参数,输入过程(见图3中右面的部分)中增环的传递系数输入正数,减环的传递系数输入负数。输入后,按下“apply”键后,程序会打开消息框,显示刚刚输入的信息,如果发现不正确或输入不完全,可以重新输入,再按下“apply”键,若正确,键下“ok”键确定即可。全部参数输入后,再选择公差分析的方法,针对这个例子,选取[经验公式法],即可输出公差分析的结果,如图3所示(图3中还应用了极值法结果作为对比)。

图3 尺寸链封闭环参数输入和尺寸链组成环闭环参数输
2计算机辅助公差查询系统
采用VC++和Access,建立国家标准的公差和配合以及偏差系列数据库,实现标准公差与配合的自动查找,快捷简单易用,免去了翻阅手册之苦。通过VC++和Access建立数据库,把国家标准公差和配合数据表格等输入计算机中。这样,建立的标准化公差数据库,,查询该库,可以方便获取不同等级和不同配合要求的标准公差数值,用于下面的计算机辅助标准化公差设计模块中。下面是建立的数据库结构和公差自动查询的界面图。
图4 标准公差库的建库与自动查询演示
公差自动查询库的使用说明:参照图4中,第一个小图和第二个小图是输入基本尺寸数值,在“公差等级”中输入公差等级代号,在“查询结果”中就可以得到对应的公差标准数值;反之,输入基本尺寸数值和公差标准值,也可以查询到对应的公差等级,即可以双向查询。第三个小图在基本尺寸中输入尺寸数值,单位是mm.在“公差”中输入公差带代码,在左边的编辑栏中输入孔的公差带代码,在右边的编辑栏中输入轴的公差带代码,输入了以后单击“开始查询”在“查询结果”中会显示两组数据,左边为对应的孔的极限偏差,右边为对应的轴的极限偏差,单位是µm;反之,输入尺寸数值和对应的孔极限偏差数值、轴极限偏差数值,可以查询得到孔和轴的配合类型。
四 实例分析
现选择一活塞发动机的装配尺寸链作为实例来分析本算法的可行性。如图3所示,当活塞上死点时,活塞顶部与汽缸头的间隙Xx变化范围为11.7mm至12.3mm,则装配技术条件为:

式中X1为汽缸体与曲轴主轴颈孔轴线的距离;X2为汽缸头垫片厚度;X3为汽缸头燃烧室深度;X4为活塞顶部至活塞销孔中心距;X5为连杆大小头孔中心距;X6为曲轴主轴颈至连杆轴颈的中心距。
已知名义尺寸
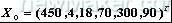 显然尺寸X2,X3具有平面加工特征,而其它四个尺寸具有定位加工特征。
显然尺寸X2,X3具有平面加工特征,而其它四个尺寸具有定位加工特征。
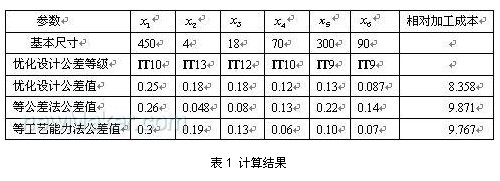
分析计算结果见表1,经优化后的尺寸链加工成本比传统公差优化设计方法节省加工成本15%。
上述讨论了基于装配成功率的计算机辅助公差优化设计数学模型,很显然公差优化设计是一种非线性不等式约束的规划问题,且是个凸规划问题。一般来说,所有适用于解决非线性约束问题的优化算法均可以采用,如可行方向法、梯度投影法、直接法、序列无约束最小方法(即SUMT,包括罚函数法、障碍函数法)、广义乘子法等等,其中,广义乘子法比较适用于公差优化设计。
五 结论
在UG环境下,通过对话框输入封闭环和各个组成环信息,再由计算机自动进行公差分配和公差分析工作,可以反复计算分析,直到满意为止;可随时修改尺寸链,增加必要组成环或者删减冗余组成环,重新分析和计算尺寸链;实现了交互性公差设计,交互输入尺寸链信息;不必先建立装配模型;保证尺寸链的正确性。这一设计尤其适用于飞机公差设计,因为飞机产品外型复杂,装配模型的建立耗时费力,而且由于其模型过于复杂,往往无法遍历该模型而得到其装配尺寸链。采用交互模式,不仅建立尺寸链方便正确,而且不需事先建立复杂的飞机装配模型,设计过程中还可以实时修改模型,交互设计。
公差标准化优化设计的研究内容,在我国的航空企业有着广泛的应用前景,有利于提高产品质量、缩短设计周期,促进先进制造、装配及检测技术的推广,为我国航空业的全机无纸数字化制造技术的发展提供基础理论和技术支持,还应该进一步开发研究飞机公差设计的优化方法。
转自:互联网
|