从误差理论到公差设计的延伸

        引 言
        目前,计算机辅助公差设计(CAT)作为CAD、CAM、CAPP乃至CIMS系统中的重要一环,倍受国内外学者重视,相继提出了不少公差设计的思想及数模,其依据的基础理论也颇丰富。基础理论与专业知识是有机结合的,由此,从误差理论的有关知识出发,导出公差设计的数学模型就是本文的宗旨。
        1 误差理论的有关知识误差的合成与分配曾从函数的系统误差及函数的随机误差出发,导出了系统误差的合成及随机误差的合成的有关公式;现以随机误差合成的有关公式为例加以阐述。
        假设测量中存在n项随机误差,且各项误差取相同的置信概率,则合成后的总误差

式中,ai———各误差的传递系数;ρij———任意两误差间的相关系数。若各项误差的置信概率不同,则合成后的总误差

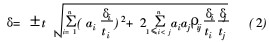
式中t、ti分别代表总误差、各单项误差的置信系数。
若各项误差服从正态分布,具有相同的置信概率,且qij=0,则合成后的总误差

        (3)式是较为广泛使用的误差合成公式。
        2 将误差理论的公式拓宽到公差设计中
        众所周知,“公差”是用来限制零件的加工制造“误差”的,如果加工制造“误差”遵循统计规律,则“公差”也可按统计公差进行设计,从这个意义上讲,公式(1)、(2)、(3)的拓宽是有其理论根据的。
        若零件的封闭环与组成环间呈线性尺寸链,即 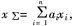,式中n为组成环的数目,ai为带正负号的各组成环对封闭环的传递系数;在各组成环按正态分布且相互独立的前提下,我们由(2)式得

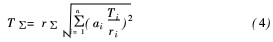
式中T∑代表封闭环公差,r∑、ri分别代表封闭环、组成环的置信系数,Ti代表各组成环公差。该式可视为公差设计的数模的一种表达式。
若考虑到零件为批量生产,且组成环与封闭环都取相同的置信概率—99.73%,这时,由(3)式得

该式是公差设计中最简单的数学模型,它可作为零件封闭环公差设计的依据。
        3 拓宽后的可行性
        由误差理论中的式(2)、(3)结合工程实际问题引出了公差设计中的式(4)、(5),这种拓宽的可行性如何呢?经查阅近期的有关杂志及书籍,发现式(4)、(5)很有其应用价值,这也证明了我们从误差理论到公差设计拓宽思路的正确性、合理性。
        4 对误差理论的再思考
        上述将基础理论知识与工程实际问题结合的思路,给我们的启迪是:概率论中正态分布的随机变量的概率密度

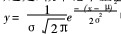中,若将x代表多次测量的测得值,则(x-μ)即是测量误差δ,于是概率论中随机变量的概率密度就是测量过程中随机误差的概率密度,即

        这样,对有关随机变量的研究就可拓宽到随机误差的领域中。
        又如,在研究n次等精度单变量测量的贝塞尔公式 时,如果理解了公式中分母(n-1)的内涵(代表自由度),就不难写出多变量(t个)等精度测量数据的标准差 t(自由度为n-t),而这样直接写出的公式与用数学手段推出的公式是完全一致的。
        再如,在误差理论中,设总误差δ为已知时按等作用原则分配各单项误差,使

D1=D2=…= )则有

式中n代表组成环数,T∑代表封闭环公差,Ti代表各组成环公差,ai意义同前)。
        按(7)式分配得到各组成环的公差值后,再按加工的可能性进行调整,将那些容易保证的项压缩,不易保证的项放宽,调整后再按公差合成公式计算T∑,使之不超过给定的T∑,如仍不能满足时,再行压缩可能压缩的公差项,直到验算能满足要求为止。
        5 结束语
        从误差理论到公差设计绝非仅局限于该二门特殊学科间的联系与结合,它所体现出的思想,完全可以映射到其它的学科领域中,而不失其一般性。

转自：互联网