|
正弦波振荡电路
在一般放大电路中,我们千方百计地避免电路发生振荡,可是在波形发生器中却完全相反,是要想方设法地让电路工作在振荡状态。虽然负反馈和正反馈电路都可能产生振荡,但正反馈电路起振相对要容易实现些,下面以正反馈电路来说明振荡电路的工作原理和仿真分析。
正反馈电路产生振荡的条件是:|AF|=1,也就是说,它应满足下面两个条件:相位平衡条件和幅值平衡条件。
相位平衡条件是放大电路的相移与反馈网络的的相移之和等于2np;幅值平衡条件是放大倍数与反馈系数的乘积之模等于1。这里所说的幅值平衡条件是指正弦波已经产生且电路已经进入稳定状态而言。
为了保证正弦波振荡电路正常工作,其电路形式应包含以下几个部分:
1. 放大电路
没有放大电路,不可能产生正弦波振荡。放大电路不仅必须有供给能量的电源,而且应结构合理,静态工作点正确以保证放大电路具有放大电路。
2. 反馈网络
其作用是形成反馈(以正反馈而言),以满足相位平衡条件。
3. 选频网络
选频网络的作用是让单一频率满足振荡条件,以产生单一频率的正弦波。选频网络所确定的频率一般即为正弦振荡电路的振荡频率。但在很多正弦振荡电路中,选频网络与反馈网络结合在一起。
4. 稳幅环节
为了使振荡电路稳定且波形好,还需要稳幅环节。
正弦波振荡电路如按选频网络的元件类型来分可分为RC正弦振荡电路,LC正弦振荡电路和石英晶体正弦振荡电路。下面我们以LC正弦振荡电路中的电感三点式和石英晶体振荡电路为例说明正弦波振荡电路的设计和分析方法。
电感三点式正弦波振荡电路
三点式电路有电容三点式和电感三点式,它们的共同特点是都从LC振荡回路中引出三个端点和晶体管的三个极或运算放大器的三个端口相连接。L1和L2串联再和C并联,在L1、L2串联成的等效电感L中,可把其连接点4看作L的中间抽头。对交流信号而言,电感两端分别接到三极管的基极和集电极,中间抽头在交流通路中相当接地,而三极管的发射极在交流通路中,经过旁路电容Ce接地,因此在交流通路相当于把发射极接,这就构成了电感的三个端点分别和三极管的三极相连接,从而此电路是电感三点式振荡电路,其交流通路等效电路如下:
Cb为隔直电容,以防VCC通过电感L2直接与三极管的基极相连。
当LC电路工作在振荡状态时回路电流比流入回路或从回路流出的电流大得多,因此谐振回路外界的影响可以忽略不计。也就是说,电感的中间抽头的瞬时电位一定在首、尾两端点的瞬时电位之间。另外,在电感三点式正弦波振荡电路中,电感的首端、中间抽头、电感的尾端中通常有一点交流接地。因此对于并联谐振频率而言,电感三个端点的相位关系有以下两种情况:
若电感的中间抽头交流接地,则首尾两端的相位相反。
若电感的首端或尾端交流接地,则电感其它两个端点的相位相同。
电感中间抽头接直流电压源,也即交流接地,属于上述第一种情况,所以电感两端的相位相反。
现在我们来分析电路的相位条件,请读者看等效电路即可。
假设从三极管的基极处断开并输入一个(+)信号,那么从三极管的集电极将输出一个(-)信号,也即电感的1端是(-)信号,而电感两端电位相反,所以在电感的3端将得到一个(+)信号,可见反馈信号与输入信号都为(+),也即表示两者同相,所以满足相位平衡条件。
电感三点式的幅值条件较易满足。只要LC并联电路的Q值和三极管的b值不要太低,而且LC并联谐振时的阻抗都比较大,一般|AF|都会比1大得多。因此只要满足相位条件一般即能起振。
电感三点式的振荡频率基本上由LC并联电路的谐振频率决定,即:
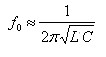
L为等效电感量,在此如果不考虑两电感之间的耦合,则有:
L=L1+L2
如果考虑两电感之间的耦合,则有:
L=L1+L2+2M
上式中,M为L1与L2之间的互感。
利用上面的几个算式,我们来计算电路的工作频率(为了简单起见,在此先不考虑互感情况)。
L=L1+L2=11mH+11mH=20mH
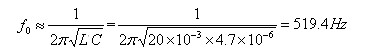
所以其振荡周期为1.93毫秒。下面我们就来仿真分析这个电路的工作情况。我们使用了一个初始条件,即电路工作之前电容C上的电压为0V。同时由上面计算可知,此振荡电路的周期约为2毫秒,一般观察电路工作5个周期以上即可。
电感三点式正弦波振荡电路不仅容易起振,而且可采用可变电容器能在较宽范围内调节谐振频率,所以在需要改变频率的场合(如收音机、信号发生器等)中得到广泛应用。但电感三点式所产生的波形含有高次谐波,且波形不够理想,因此在更高要求的电路中,将使用晶振。
转自:维库电子市场网
|